Zénon d'Éléa est un logicien et philosophe grec qui est principalement connu pour les paradoxes nommés en son honneur. On ne sait pas grand-chose de sa vie. La ville natale de Zeno est Elea. Toujours dans les écrits de Platon, la rencontre du philosophe avec Socrate a été mentionnée.
Vers 465 avant JC e. Zeno a écrit un livre dans lequel il a exposé toutes ses idées. Mais, malheureusement, il n'a pas atteint nos jours. Selon la légende, le philosophe est mort dans une bataille avec un tyran (vraisemblablement le chef d'Eléa Nearch). Toutes les informations sur Elea ont été recueillies petit à petit: à partir des travaux de Platon (né 60 ans plus tard Zénon), d'Aristote et de Diogène Laertius, qui écrivit trois siècles plus tard un livre de biographies de philosophes grecs. Zeno est également mentionné dans les écrits des derniers représentants de l'école de philosophie grecque: Thémisty (4ème siècle après JC), Alexander Afrodinsky (3ème siècle après JC), ainsi que Philoponus et Simplicius (tous deux vivaient au 6ème siècle après JC).. De plus, les données de ces sources sont si bien cohérentes entre elles que toutes les idées du philosophe peuvent être reconstruites à partir de celles-ci. Dans cet article, nous vous parlerons des paradoxes de Zeno. Commençons donc.

Paradoxes de l'ensemble
Depuis l'ère de Pythagore, l'espace et le temps étaient considérés exclusivement du point de vue des mathématiques. Autrement dit, ils étaient censés être composés de nombreux points et points. Cependant, ils ont une propriété plus facile à détecter qu'à définir, à savoir la «continuité». Certains paradoxes zénon prouvent qu'il ne peut pas être divisé en moments ou en points. Le raisonnement du philosophe se résume à ce qui suit: «Supposons que nous ayons achevé la division jusqu'au bout. Alors une seule des deux options est vraie: soit nous obtenons les quantités minimales possibles ou des pièces qui sont indivisibles, mais infinies en quantité, ou la division nous conduira à des pièces sans ampleur, car la continuité, étant homogène, doit être divisible en toutes circonstances. Il ne peut pas être divisible dans une partie, mais pas dans l'autre. Malheureusement, les deux résultats sont assez ridicules. Le premier est dû au fait que le processus de division ne peut pas se terminer tant qu'il y a des parties dans le reste qui ont une valeur. Et le second est parce que dans une telle situation, au départ, le tout aurait été formé à partir de rien. » Simplicius a attribué cet argument à Parménide, mais il est plus probable que son auteur soit Zeno. Nous allons plus loin.
Paradoxes du mouvement de Zeno
Ils sont considérés dans la plupart des livres consacrés au philosophe, car ils entrent en dissonance avec la preuve des sentiments des Eléatiques. Par rapport au mouvement, on distingue les paradoxes zénos suivants: «Flèche», «Dichotomie», «Achille» et «Étapes». Et ils sont venus vers nous grâce à Aristote. Examinons-les de plus près.
Flèche
Un autre nom est le paradoxe quantique de Zeno. Le philosophe affirme que toute chose reste immobile ou bouge. Mais rien n'est en mouvement si l'espace occupé lui est égal en longueur. À un certain moment, la flèche en mouvement est au même endroit. Par conséquent, il ne bouge pas. Simplicius a formulé ce paradoxe sous une forme courte: «Un objet volant occupe une place égale dans l'espace, mais ce qui prend une place égale dans l'espace ne bouge pas. Par conséquent, la flèche est au repos. " Femistius et Phelopon ont formulé des options similaires.
"Dichotomie"
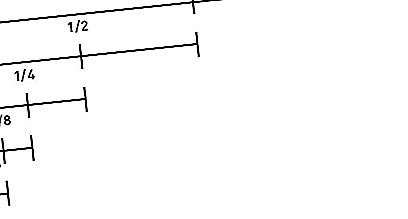
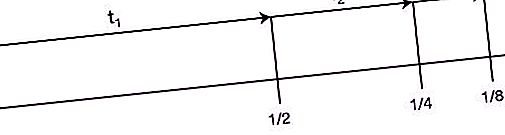
Prend la deuxième place dans la liste des "Zeno Paradoxes". Il se lit comme suit: «Avant qu'un objet qui commence à se déplacer puisse parcourir une certaine distance, il doit surmonter la moitié de ce chemin, puis la moitié du reste, etc. à l'infini. Puisque lors de divisions répétées de la distance en deux, le segment devient tout le temps fini, et le nombre de ces segments est infini, cette distance ne peut pas être surmontée en un temps fini. De plus, cet argument est vrai à la fois pour les petites distances et les vitesses élevées. Par conséquent, tout mouvement est impossible. Autrement dit, le coureur ne pourra même pas démarrer."
Ce paradoxe a commenté en détail Simplicius, indiquant que dans ce cas, un nombre infini de touches doit être effectué dans un temps fini. "Quiconque touche à n'importe quoi peut compter, mais l'ensemble infini ne peut pas être trié ou compté." Ou, comme le dit Philopon, un ensemble infini est indéfinissable.
Achille
Aussi connu comme le paradoxe de la tortue Zeno. C'est l'argument philosophique le plus populaire. Dans ce paradoxe du mouvement, Achille participe à une course avec une tortue, qui se voit attribuer un petit handicap au départ. Le paradoxe est que la guerrière grecque ne pourra pas rattraper la tortue, car d'abord elle atteindra le lieu de son départ, et elle sera déjà au point suivant. Autrement dit, la tortue sera toujours en avance sur Achille.
Ce paradoxe est très similaire à une dichotomie, mais ici la division infinie va selon la progression. Dans le cas d'une dichotomie, il y a eu régression. Par exemple, le même coureur ne peut pas démarrer, car il ne peut pas quitter son emplacement. Et dans la situation avec Achille, même si le coureur commence à bouger, il ne viendra toujours pas courir n'importe où.
"Stage"
Si nous comparons tous les paradoxes de Zeno en termes de complexité, ce serait le gagnant. Il est plus difficile que d'autres d'exposer. Simplicius et Aristote ont décrit ce raisonnement de manière fragmentaire, et on ne peut pas compter sur sa fiabilité avec 100% de certitude. La reconstruction de ce paradoxe a la forme suivante: soit A1, A2, A3 et A4 sont des corps immobiles de taille égale, et B1, B2, B3 et B4 sont des corps de même taille que A. Les corps B se déplacent vers la droite pour que chaque B passe Et en un instant, ce qui est la plus petite période de temps possible. Soit B1, B2, B3 et B4 des corps identiques à A et B, et se déplace par rapport à A vers la gauche, surmontant chacun des corps en un instant.
De toute évidence, B1 a surmonté les quatre corps de B. Prenons pour une unité le temps qu'il a fallu à un corps de B pour traverser un corps de B. Dans ce cas, quatre unités étaient nécessaires pour tout mouvement. Cependant, on pensait que les deux moments qui s'étaient écoulés pour ce mouvement étaient minimes et donc indivisibles. Il s'ensuit que quatre unités indivisibles sont égales à deux unités indivisibles.